Miller index ↩

aliases: []
shorthands: {}
created: 2021-10-31 15:45:37
modified: 2022-06-05 19:33:10

Motivation

In a Bravais lattice, a lattice plane can be exactly determined using three noncolinear lattice points. Due to the translational symmetry, we can use only three integers to describe a lattice plane.

A lattice plane described by these indices:

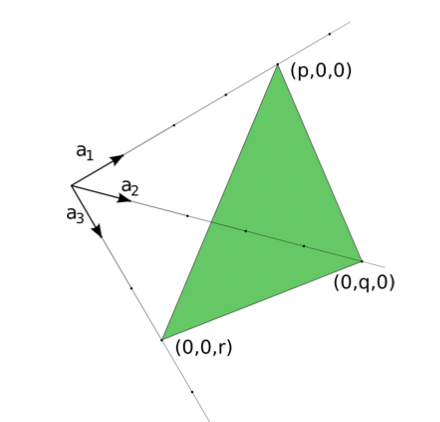
These indices can be gathered by choosing the closest plane to the origin, then find the intersection points along the lines of the primitive vectors: , and .

A given describes an infinite amount of lattice planes. These planes can also be numbered: the plane goes through the origin and the closest ones are numbered . So we can see that to every index triplet, we can assign an infinite number of lattice planes. The set of these planes is called the lattice plane set.

Miller indices

We can describe a lattice plane set instead of the indices like this:

We take the smallest possible integer triplet for which:

These new indices are called the Miller indices of the lattice plane set.

Normal vector of a lattice plane

Let's consider a lattice plane with Miller indices . The normal vector of this plane is the following reciprocal lattice vector:

This means that we can describe a lattice plane set with a given direction using a reciprocal lattice vector. (Note: different reciprocal lattice vectors describe different lattice plane sets if they are not a scalar-multiple of each other (they are not linearly dependent)).

Distance of lattice planes

Let's consider two neighboring planes in a lattice plane set with numbers and . They intersect with the crystallographic axis of in points and . The distance's projection to the normal of the planes has the length:

This is the distance between neighboring planes in the lattice plane set of Miller indices .

Examples

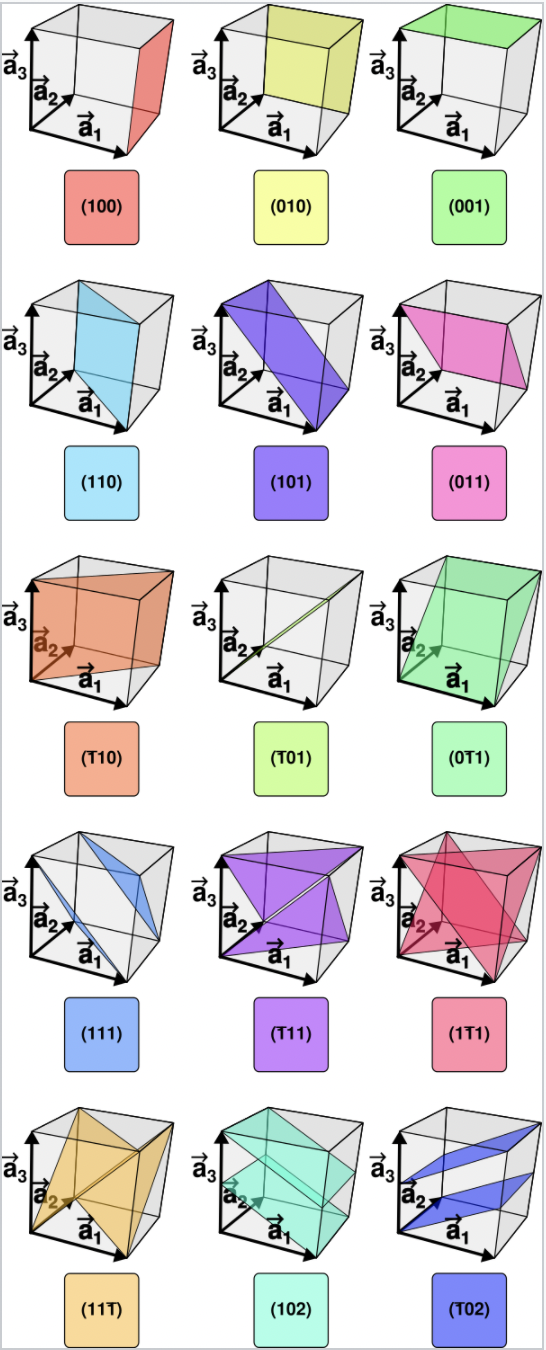
Lattice planes with different Miller indices in cubic crystals: